java - 序列中2个项目之间的最小值

Question

我正在尝试制作一个程序，它将在o（n）时间内保存数组中的一系列数字，以便快速（o（logn））回答以下问题。
min（int i，int j）：返回positions i和j之间的序列中的最小值position。
例如，如果序列是A=（22，51，83，42，90，102，114，35），我调用min（3，6）
它将返回4，因为42<83,90102。
我知道如果序列的值没有排序，就不可能实现快速时间，而且因为我想实现O（logn），所以我考虑实现一个二叉树。
问题是，我无法找出应该以何种方式将序列的值放在二叉树中，以便快速访问它们，以使min（）按需工作。

Answer 1

这是一个典型的需要用区间树来解决的问题。您可以在O(n)时间内构造它，然后在O(log n)中运行查询。
一般的想法是将一个完美的二叉树存储在一个数组中，其中索引i处的节点的子节点位于索引2i和2i+1处在叶中存储序列的值，对于每个非叶节点，存储其所有子节点的最小值。如果你从叶子向上构建树，你可以在O(n)时间内完成。
要运行间隔[a; b]的查询，可以采用两种基本方法（都在O(log n)时间内工作）：
从叶子向根部移动a和b
从根开始递归地向下移动树
两种方法的描述，你可以很容易地在互联网上的“间隔树”词组下找到。对于你的问题，我绝对推荐前一个，因为它应该快一点。
根据要求，我已经用查询树的说明扩展了我的答案让我们仔细看看我为您的问题建议的自下而上的方法。我假设数组的索引从0到n - 1。我还假设对于一些自然的n，2^k等于k如果不是，则通过在底层末尾添加+Inf元素以查询最小值，将其增加到最接近的2次方。它不会影响任何有效的查询，您会得到一个完美的二叉树，可以像我前面描述的那样轻松地索引。为了获得一个舒适的实现，我建议使用索引1作为根目录，这也适用于此描述。
这张图应该更清楚些。底部的黑色索引是原始数组的索引。每个节点旁边的绿色索引是树中的索引。现在忽略矩形，因为它们与查询示例有关。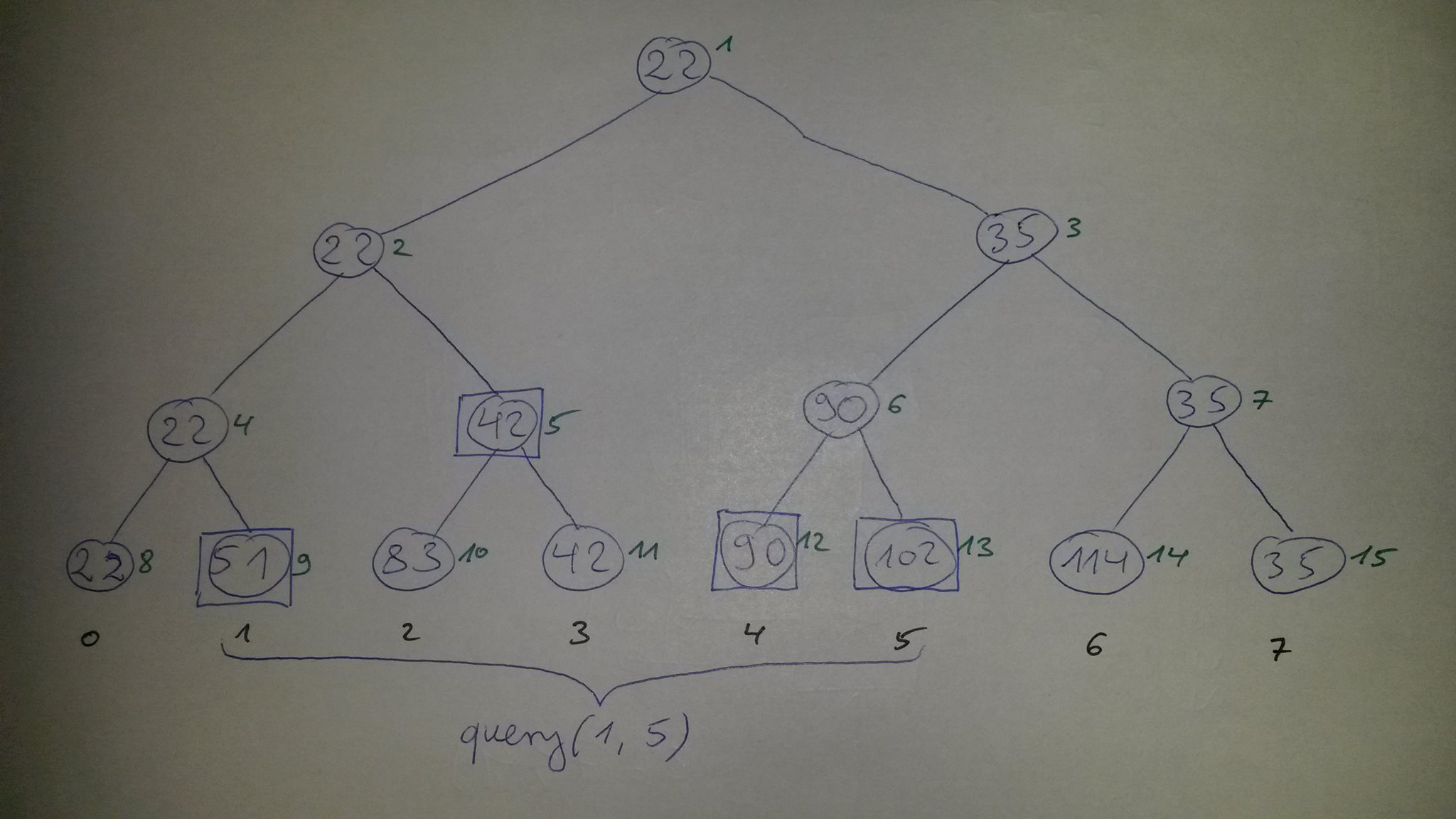

通过query(a, b)我们将表示对间隔[a; b]中的最小值（包括）的查询。首先，有一个特殊情况：当a等于b时，我们只返回tree[n + a]（请注意，当tree[1]是根时，这是正确的索引）。
当a != b时，让我们转到更复杂的情况。该算法的思路是将任意区间分割成无公共元素且完全覆盖原区间的基区间。每个基本间隔的大小是2的幂，每个基本间隔由我们的一个节点表示当我们列出所有相关的时间间隔时，我们只需要取它们节点的最小值就可以得到O(log n)的答案。
现在我们将描述选择基区间的方法在示例图像中，它们都被矩形包围。请查看以下代码段：

int x = a + n;
int y = b + n;
int result = Math.min(tree[x], tree[y]);

while (x / 2 != y / 2) {
    if (x % 2 == 0) {
      result = Math.min(result, tree[x + 1]);
    }
    if (y % 2 == 1) {
      result = Math.min(result, tree[y - 1]);
    }

    x /= 2;
    y /= 2;
}

首先，我们将原始索引转换为树中的索引。然后我们考虑包含查询边界的单个项目间隔。记住，当query(a, b)时，我排除了特殊情况。
算法按如下步骤进行，向上移动树。每当a == b时，我们都会考虑树中x % 2 == 0的同辈的间隔请检查此同级始终包含在间隔x中。与我们对[a; b]所做的相同，只是兄弟姐妹在y % 2 == 1的左侧。当y时，这意味着x / 2 == y / 2和x现在是兄弟，我们应该停止算法您可以自己检查这种方法是否以完全覆盖y的方式选择间隔。
请注意，我们最多可以检查树底部的4个节点在相互级别上，我们将检查不超过2个节点。由于树的[a; b]级别，我们可以看到任何查询的时间复杂度都是O(log n)。
奖励-修改数组您描述的问题不需要修改数组，但在基本情况下，它非常干净，我将在这里添加它。如果您还想处理O(log n)指令，这意味着set(a, v)您可以在array[a] = v时间内轻松完成首先设置O(log n)，然后向根更新路径上的最小值。